In this tutorial we will learn to solve Sudoku using Crook's pencil-and-paper algorithm.
Introduction
A Sudoku board generally consists of (9 rows x 9 columns) 81 cells. And the board is divided into 9 sub boards each having (3 rows x 3 columns) 9 cells.
You can find them on newspapers, magazines or even as a puzzle books. It looks like the following.
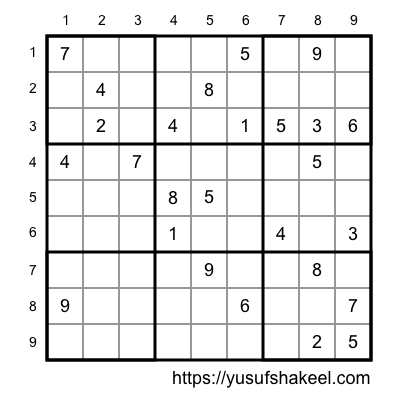
Sub boards
Following are the row and column ranges of each of the 9 sub boards that appear in a 9x9 Sudoku board.
+-----------+-----------+---------+--------------+------------+
| Sub board | Start Row | End Row | Start Column | End Column |
+-----------+-----------+---------+--------------+------------+
| 1 | 1 | 3 | 1 | 3 |
+-----------+-----------+---------+--------------+------------+
| 2 | 1 | 3 | 4 | 6 |
+-----------+-----------+---------+--------------+------------+
| 3 | 1 | 3 | 7 | 9 |
+-----------+-----------+---------+--------------+------------+
| 4 | 4 | 6 | 1 | 3 |
+-----------+-----------+---------+--------------+------------+
| 5 | 4 | 6 | 4 | 6 |
+-----------+-----------+---------+--------------+------------+
| 6 | 4 | 6 | 7 | 9 |
+-----------+-----------+---------+--------------+------------+
| 7 | 7 | 9 | 1 | 3 |
+-----------+-----------+---------+--------------+------------+
| 8 | 7 | 9 | 4 | 6 |
+-----------+-----------+---------+--------------+------------+
| 9 | 7 | 9 | 7 | 9 |
+-----------+-----------+---------+--------------+------------+Note! There are other variations of Sudoku puzzle as well. The 9x9 Sudoku is one of the popular boards.
Rules of Sudoku puzzle
Following are the rules that we must follow all the time while solving a 9x9 Sudoku board.
- Use only number 1 to 9 to fill the cells.
- If a number is filled in a cell then:
- that number should not reappear in that row.
- that number should not reappear in that column.
- that number should not reappear in that sub board.
Example: Consider cell (Row 2, Column 2) with value 4. This means 4 should not reappear in row #2, column #2 and sub board #1.
Cell
We denote a cell of Sudoku puzzle board like the following C(r,c) where r is the row and c is the column.
Crook's pencil-and-paper algorithm
Professor J. F. Crook of Computer Science at Winthrop University, created this algorithm that solves Sudoku puzzles.
In order to solve a 9x9 board using Crook's algorithm we need to first understand few things.
Mark up of a cell
The mark up of a cell is a set of numbers that it can possibly contain.
Lets take an example. In the following image the mark of cell C(1,2) is 1368. This means we can fill cell C(1,2) with any one of the number 1, 3, 6 or 8.
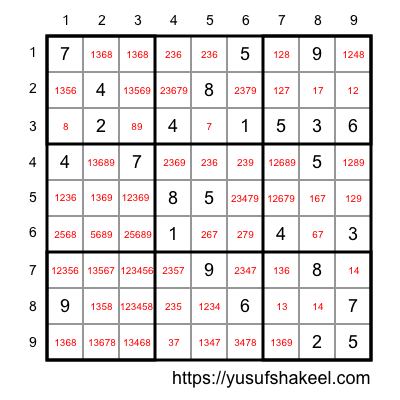
What does mark up of a cell tell us?
If we look at the above mark-ups we can clearly see that some cells have only 1 number like C(3,1). We can also see that there are cells with 2 numbers like C(2,8).
So, lesser the numbers in a cell mark up, higher the confidence of solving it.
For example, if mark up of a cell has 5 numbers then confidence of solving it is 100/5 = 20%. Cell C(2,3) has 5 numbers in its mark up {1, 3, 5, 6, 9} so we are 20% confident.
Similarly, if we look at cell C(3,1), it has only 1 number in its mark up 8. This means we are 100% confident.
Solving tip #1 - This solves most of the easy puzzles
Step 1: Create mark up of each empty cell.
Step 2: Find all the cells with only 1 number in their mark-up and fill them.
Now repeat Step 1 and Step 2 till all cells are filled.
For hard puzzles we need to know about a preemptive set.
Preemptive set
Preemptive set is a set that consists of a list of N numbers and a list of N cells.
{[N numbers], [N cells]} where, N is between 2 to 8.Each of the N numbers can be between 1 and 9 (both inclusive). And the criteria is that no numbers apart from that N numbers can occupy those N cells.
Preemptive sets are created using the mark-ups.
Preemptive set in a row
If we have a preemptive set {[3, 4], [C(3,3), C(3,6)]}.
This means mark up of cell C(3,3) and C(3,6) is {3, 4}. It also means number 3 and 4 cannot appear in any other cells in Row #3. So, we can remove number 3 and 4 from mark up of all the other cells in Row #3.
Preemptive set in a column
If we have a preemptive set {[7, 8], [C(4,7), C(6,7)]}.
This means mark up of cell C(4,7) and C(6,7) is {7, 8}. It also means number 7 and 8 cannot appear in any other cells in Column #7. So, we can remove number 7 and 8 from mark up of all the other cells in Column #7.
Preemptive set in a sub board
If we have a preemptive set {[6, 7], [C(1,1), C(3,3)]}.
This means mark up of cell C(1,1) and C(3,3) is {6, 7}. It also means number 6 and 7 cannot appear in any other cells in sub board #1. So, we can remove number 6 and 7 from mark up of all the other cells in sub board #1.
Solving tip #2 - This solves most of the medium to hard puzzles
Run through Step 1 to Step 2 mentioned in section Solving tip #1
If no cell was filled in Step 2 then move to step 3.
Step 3: Find preemptive sets. Select a preemptive set that has a smaller set of numbers. Clear out mark up of other cells using the preemptive sets.
Step 4: If there are at least one cell whose mark up consists of one number than fill that cell and go to Step 1.
Most of the middle to hard puzzles will get solved by now.
If after following all the above steps we are unable to find a cell whose mark up has one number, then we will go to Solving tip #3.
Solving tip #3 - Backtracking - This solves all
Run through Step 1 to Step 4 mentioned in section Solving tip #1and Solving tip #2.
Step 5: If we are at a point were no cells exist whose mark up has only one number than we will pick one of the cells with the smallest number of mark up. Then we will fill that cell with one of the number from its mark up and go to Step 1 and repeat till the board is solved.
Step 6: If we reach a point were the board becomes invalid then we will backtrack to the cell were we picked one of the number from its mark up. Now we will pick the next number from the mark-up of that cell and repeat from Step 1.
Example:
The following board has no cells whose mark up has only one number.
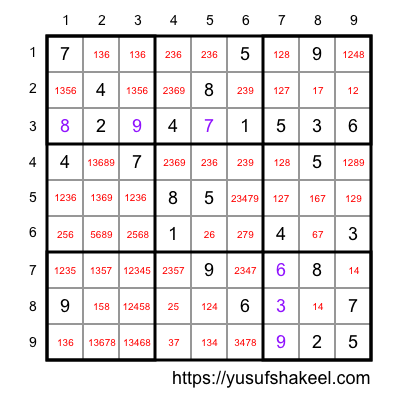
In this case let's pick cell C(2,8) having mark up {1, 7}. Here we pick say 1 from its mark up and fill the cell. Now we go to Step 1 and repeat. If we reach a point were the board becomes invalid then be backtrack and repeat.
Since cell C(2,8) has two numbers {1, 7} in its mark up so, we first pick 1 and try to solve the board. If we fail, then we backtrack to cell C(2,8) and pick 7 and repeat. By this time the board should get solved.
Note if the board has invalid input to begin with then we won't be able to solve the board.
Solution
If you want to try out solving 9x9 Sudoku puzzles then you can check out SudokuBox. It is an open source project available on GitHub. It is written in JavaScript and you can give it a try.
You can also add it to your Node projects by running npm i sudokubox command.
Reference
- A Pencil-and-Paper Algorithm for Solving Sudoku Puzzles
- SudokuBox is an open source project that solves 9x9 sudoku puzzle. This project is written in JavaScript.
